Vi phân, tích phân, đạo hàm là phần kiến thức đại số hết sức quen thuộc với các học sinh lớp 12. Nếu đã từng hoàn thành chương trình THPT, bạn hẳn đã từng làm quen với công thức tổng quát Dy/Dx. Vậy chính xác thì Dy/Dy là gì?
Ôn lại kiến thức về vi phân
Trước khi khi đi sâu phân tích khái niệm Dy/Dx là gì, Beat Đầu Tư sẽ giúp bạn ôn lại chút lý thuyết về vi phân.

Trong đại số, phân có thể xem như một nhánh xuất phát từ vi tích phân. Nó liên quan đến đến việc nghiên cứu sự thay đổi của hàm số khi biến số bắt đầu biến đổi.
Đối tượng nghiên cứu chủ yếu trong việc phân tính đạo hàm của một hàm số. Trong đó, đạo hàm tại một điểm tương ứng với giá trị đầu vào hãy được tính là điểm gốc để so sánh hàm số gần nhất.
Còn nếu xem xét trên màn hình học trực quan thì đạo hàm tại một điểm tiếp tuyến của hệ số góc của đường tiếp tuyến đến ứng với đồ thị hàm số tại chính điểm đó. Tuy nhiên để điều này xảy ra thì điều kiện phải là đạo hàm có tồn tại và xác định tại điểm đó.
Dy/Dx là gì?
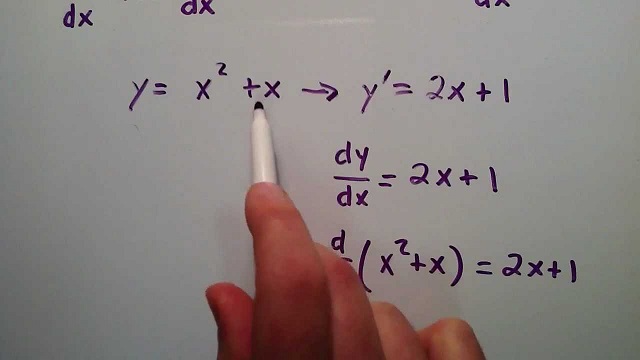
Để trả lời thắc mắc Dy/Dx là gì, chúng ta sẽ cùng nhau nhận xét hàm số y = f(x). Đạo hàm hàm số y, tạo kí hiệu là y’. Nó mô tả sự biến thiên tạm thời của hàm số f(x), xét tại điểm x cụ thể. Giá trị đạo hàm của hàm số y tại điểm x0 được xem như giá trị độ dốc ứng với đường tiếp tuyến của hàm số y tại điểm x0.
- Trường hợp x0 tăng, f”(x0) > 0
- Trường hợp x0 giảm, f”(x0) < 0
Đạo hàm cho biết tính phụ thuộc của hai chiều đại lượng. Chẳng hạn như ký tự trên khi x tăng thì y cũng tăng, và ngược lại. Câu hỏi đặt ra lúc này là làm sao mô tả chính sự biến thiên tạm thời của hàm số y tại điểm x0.
Sự biến thiên tạm thời xét tại điểm x0 ông cũng đồng thời là sự biến thiên của hàm số y trong trường hợp điểm x di chuyển một khoảng từ x0 đến x1. Chúng ta tạm ký hiệu x1 – x0 = Dx. Lưu ý, Dx có thể tiến sát nhưng không bao giờ bằng 0.
Có nghĩa đạo hàm của hàm số y tại điểm x0 sẽ là y” = f(x) – f(x0) khi Dx dịch chuyển dần tới 0.
Nếu xem xét tuổi trên mặt hình học, đạo hàm của hàm số số f(x) tại điểm x0 có thể coi như hệ số góc ứng với đường tiếp tuyến có hàm số y = f(x0).
Trường hợp hàm số f(x) sở hữu đường tiếp tuyến với điểm x0, đạo hàm tại điểm x0 mới tồn tại. Nếu như không đáp ứng điều kiện này, đạo hàm tại điểm x0 cũng không tồn tại.
Như vậy, chúng ta có công thức đạo hàm tổng quát y” = f'(x) = Dy / Dx. Đến đây, định nghĩa Dy/Dx là gì có lẽ đã phần nào được Beat Đầu Tư giải thích rõ. Trong mục tiếp theo, chúng ta sẽ tiếp tục tìm hiểu một số kiến thức liên quan đến đạo hàm.
Phân tích hệ số góc, đạo hàm cấp 2
Trong phần đầu tiên, bạn đã được tìm hiểu về định nghĩa Dy/Dx là gì. Còn ở mục dưới đây, Beat Đầu Tư sẽ cùng bạn phân tích một số khái niệm có liên quan đến công thức này.
Hệ số góc
Hệ số góc hay còn được gọi là độ dốc cho biết hàm số số tại điểm xác định nào đó đó đã tăng hay giảm.
Ngoài ra, hệ số góc của đường thẳng tại một mặt phẳng bất kỳ còn được hiểu là tỷ lệ giữa sự biến động của tọa độ y trên sự biến động tọa độ x. Định nghĩa này có thể điều trị ngắn gọn thông và công thức m = ∆y∆x = tan(θ).
Để tính toán hệ số góc của tiếp tuyến ứng với hàm số f(x) tại điểm x0, bệnh cần tính đạo hàm của hàm số theo công thức vừa nêu ở mục trên. Thông thường khi hệ số góc càng lớn thì hình số lại biến động càng nhanh, và ngược lại.
Đạo hàm cấp 2
Dựa vào đạo hàm cấp 2 của hàm số 2 đồ thị f(x) tại điểm x0 sẽ cho bạn biết đường cong của đường cong của f(x) đang đi lên hay đi xuống. Dựa vào dấu hiệu này, bạn có thể tính toán giá trị Min và Max của đồ thị.
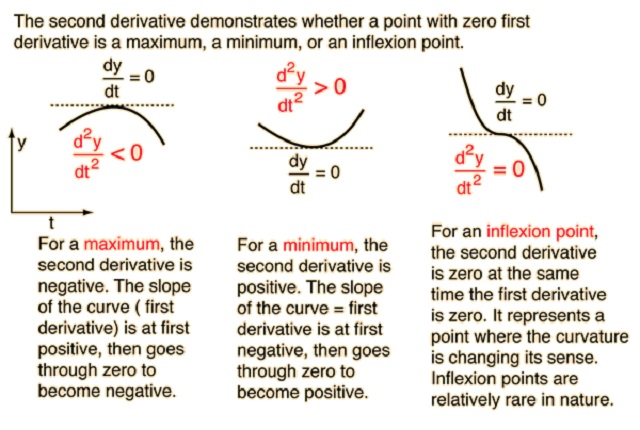
Để tính đỉnh của đồ thị, bạn cần tính đạo hàm cấp 1 tại điểm 0, bởi đồ thị bắt đầu đảo chiều khi f”(x) bằng 0. Tuy nhiên, vấn đề đặt ra lúc này là chúng ta lại không biết đồ thị chính xác đang đi lên hay đi xuống.
Trường hợp đồ thị f(x) di chuyển đi xuống rồi lại đi xuống có nghĩa đường cong của đồ thị tại phần đỉnh đang cong lên phía trên. Tương ứng với giá trị tại đỉnh là nhà Min (giá trị nhỏ nhất). Trong trường hợp ngược lại khi đồ thị đảo chiều từ trên xuống dưới có nghĩa đường cong của đồ thị đang hướng xuống. Lúc này, bạn cần tiếp tục tính toán đạo hàm cấp 2.
Công thức tổng quát của đạo hàm cấp 2 sẽ là y”” = Dy / Dx” = D2y / D2x.
Tổng kết
Hy vọng qua bài viết trên đây, thắc mắc Dy/Dx là gì đã được Beat Đầu Tư giải thích rõ. Rất mong rằng với chút chia sẻ của chúng tôi phần nào giúp bạn ôn lại chút kiến thức lý thú